Areas Under Curves


Back to Integration Topics Page


What does area under a curve mean?

Now you have to combine all of the concepts you have learnt so far in to finding the area under a curve. The phrase area under a curve is reffering to the following:

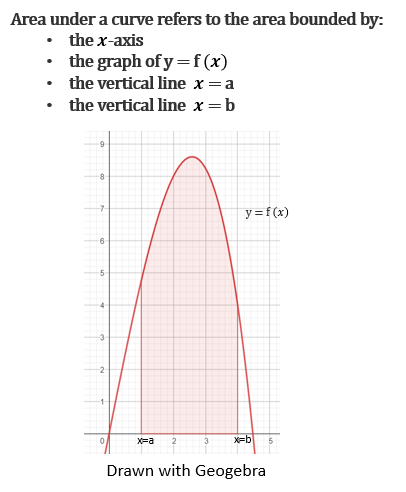
Therefore the following formula can be used to find the area:

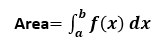
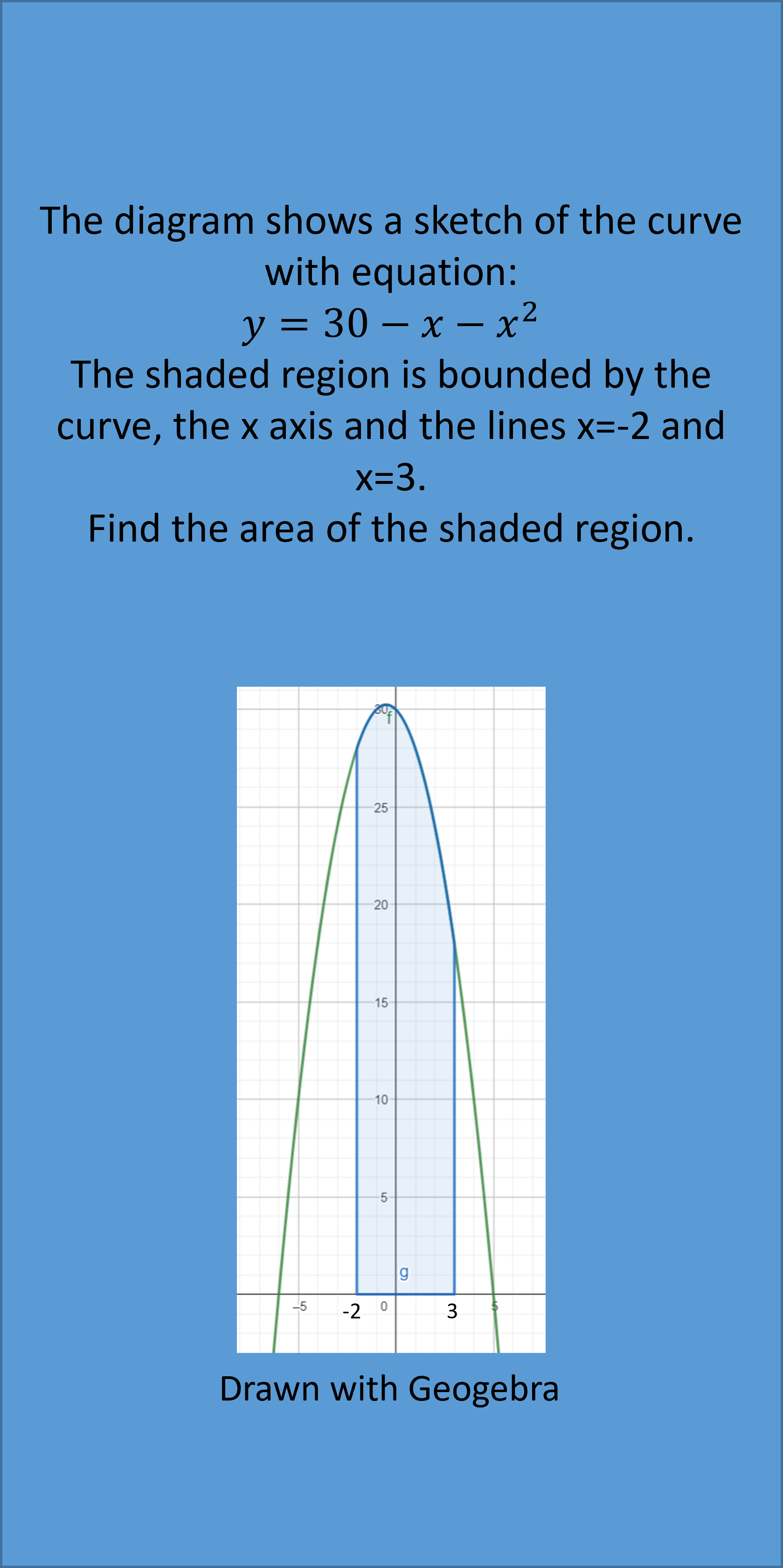
Example 1:

Example 1
Answer 1
Example 2
Answer 2

Sometimes you can get questions where the area is under the x axis. The process is the same but since the result of the definite integral is negative and area can't be negative, you take the modulus of the result. The formula above can rewritten for this case as shown below:

Example 2:

Example 1
Answer 1
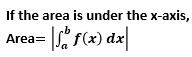
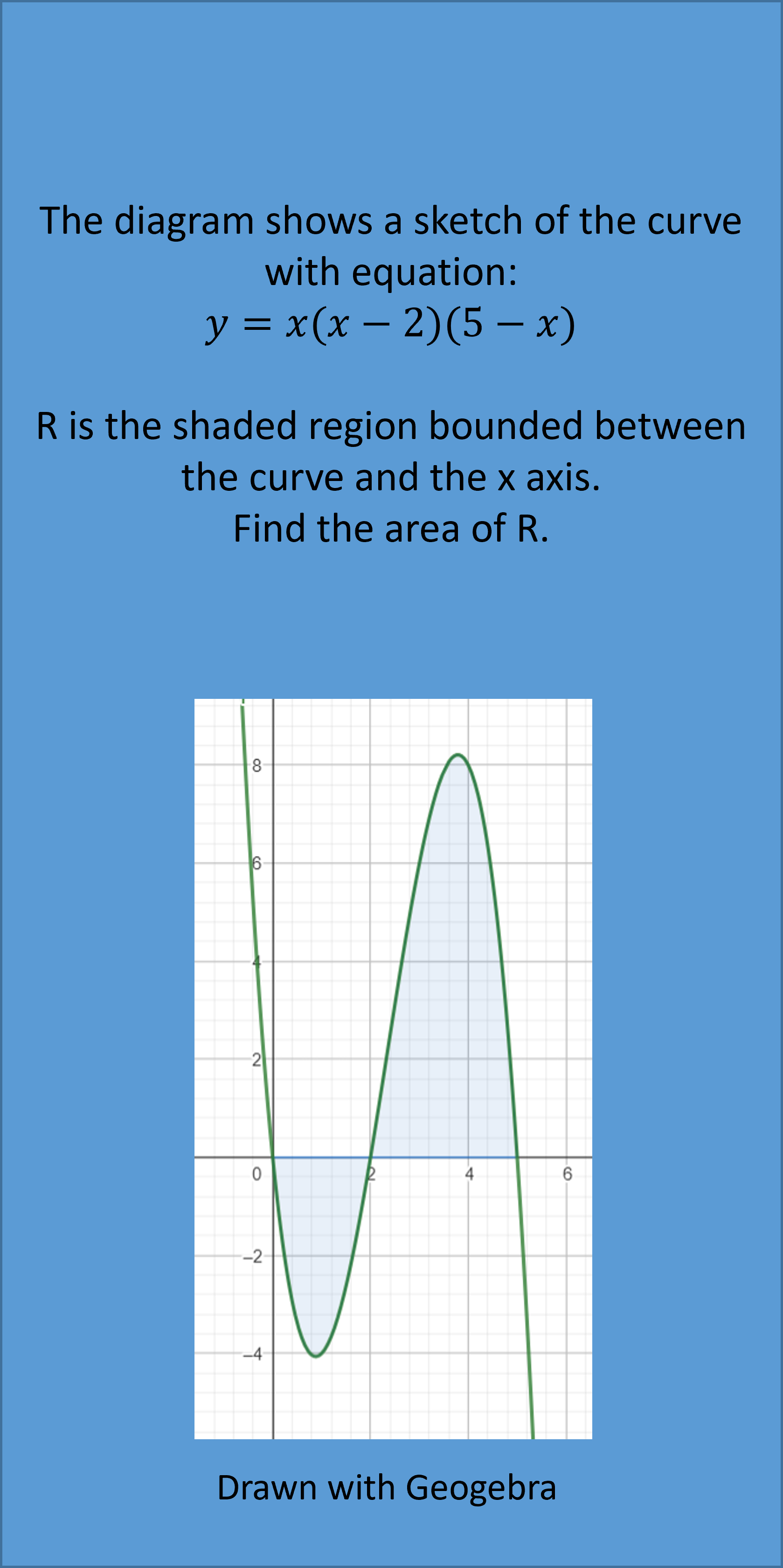
Example 2
Answer 2

If the question gives a sketch of a curve/a situation where there are areas above and below the x axis, you have to find the areas seperately and them add them together for the final answer.

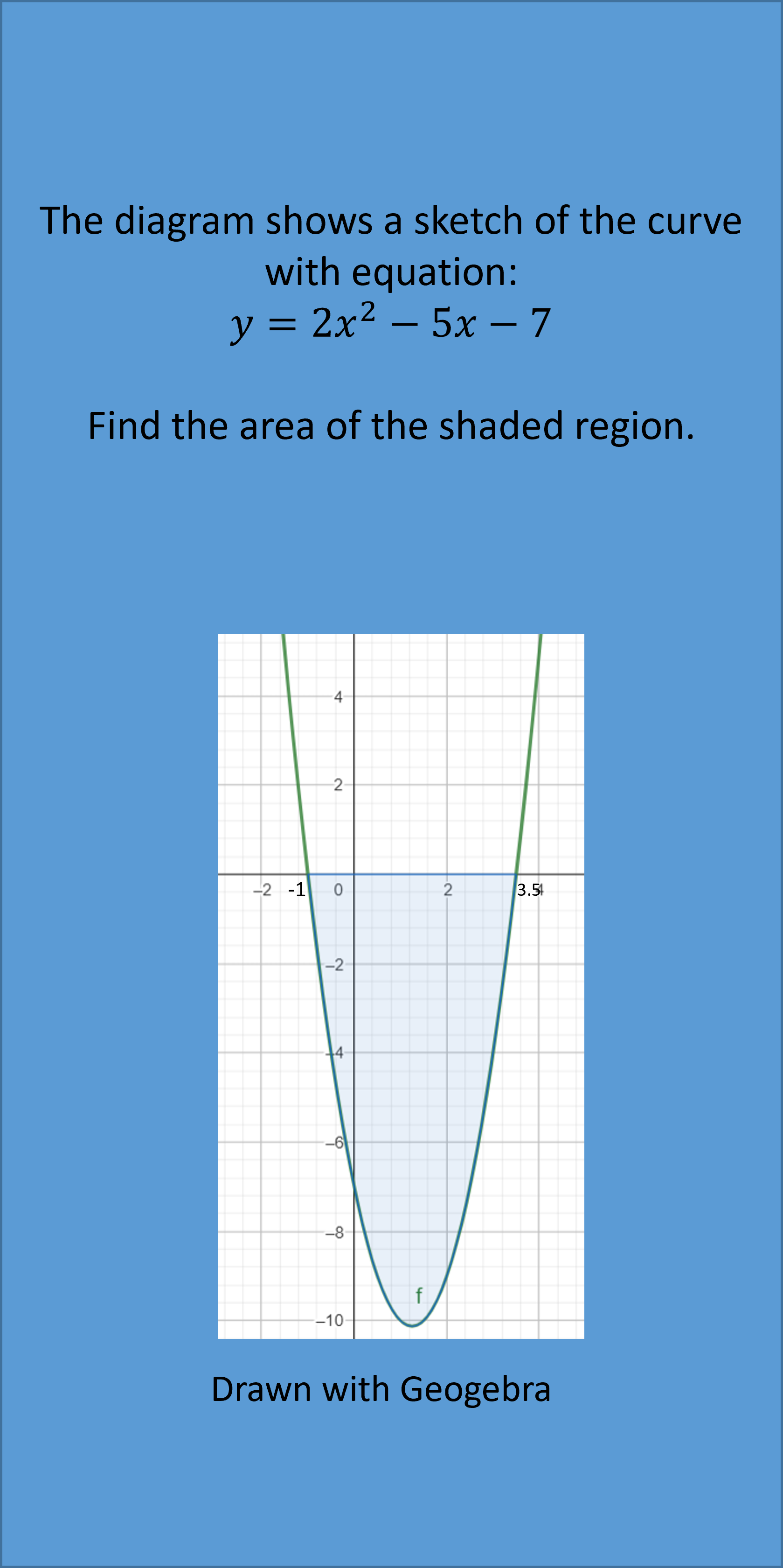
Example 3:

Example 1
Answer 1
Example 2
Answer 2

Note: The digram is a very important part to answering a question similar to example 3. If you are not given it, you should make a sketch so you can visualise which areas are below or above the x axis. This is very important as for example for example 3 if 0 and 5 is used as the limits of 1 integral only, the minus will not be considered and the answer will be lower than expected.

Areas between curves and lines

You could get cases in which you have a curve and a line and you will have to calculate the area between the curve and the line. For these questions, the diagram is the most important thing to consider. Whether it is given to you (most likely it will be) or you have to make a sketch yourself, it will make it easier to split it into shapes, in which you calculate the areas sperately and do a final calculation to find the final result.

Example 4:

Example 1
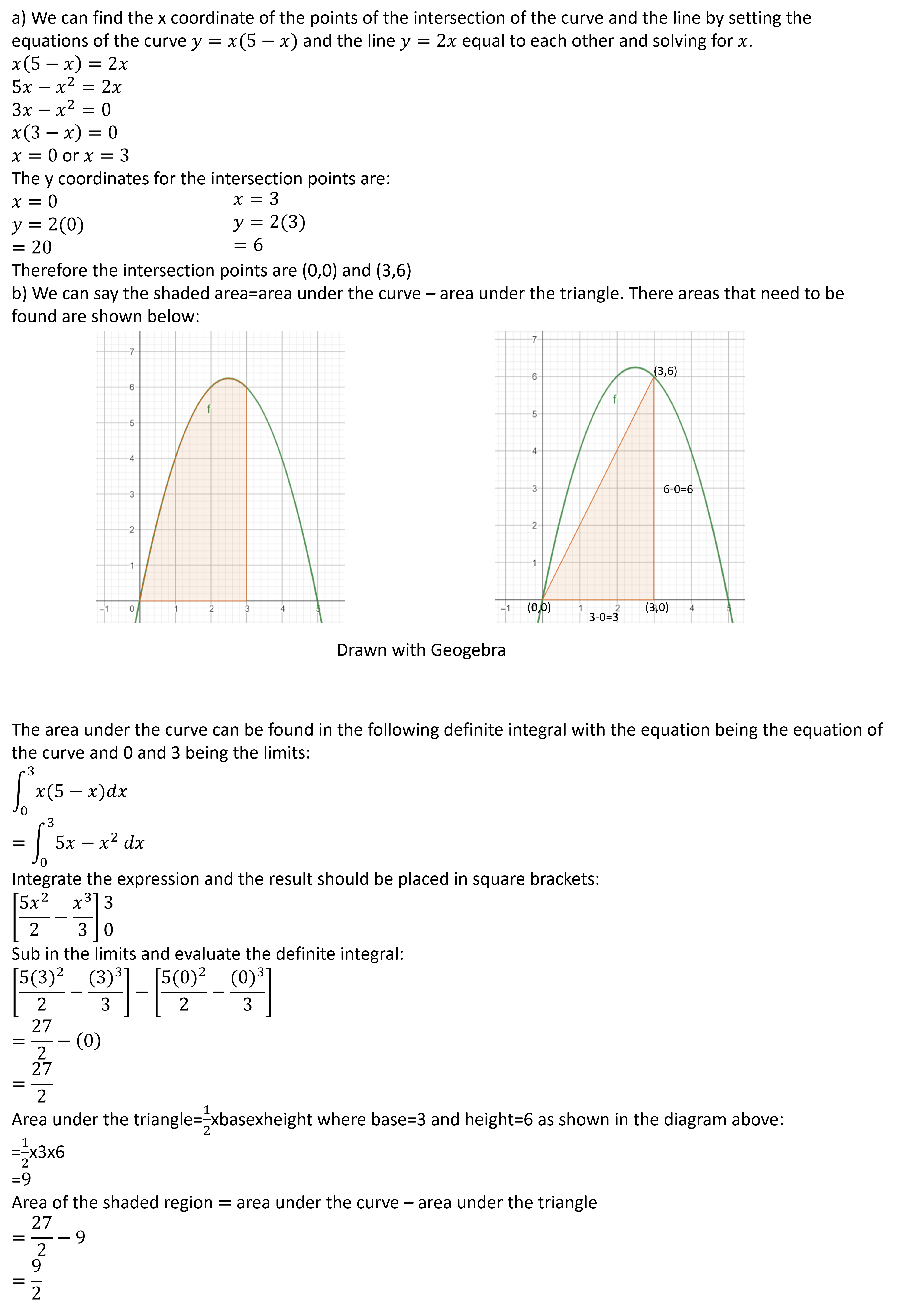
Answer 1
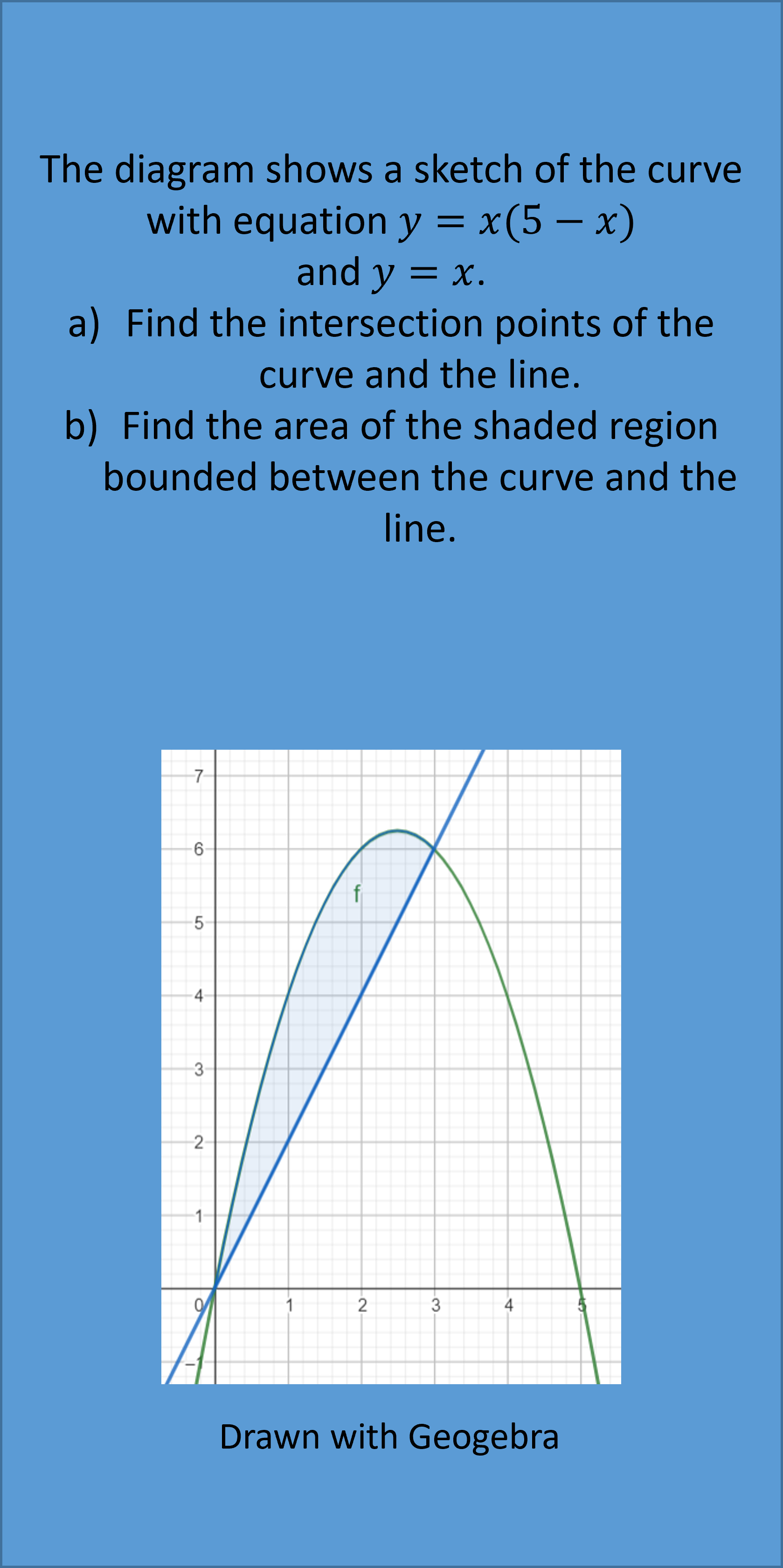
Example 2
Answer 2

Note: You will need to recap the area of different shapes like triangle, trapezium and rectangle/square, for these types of questions.

Practice Question:





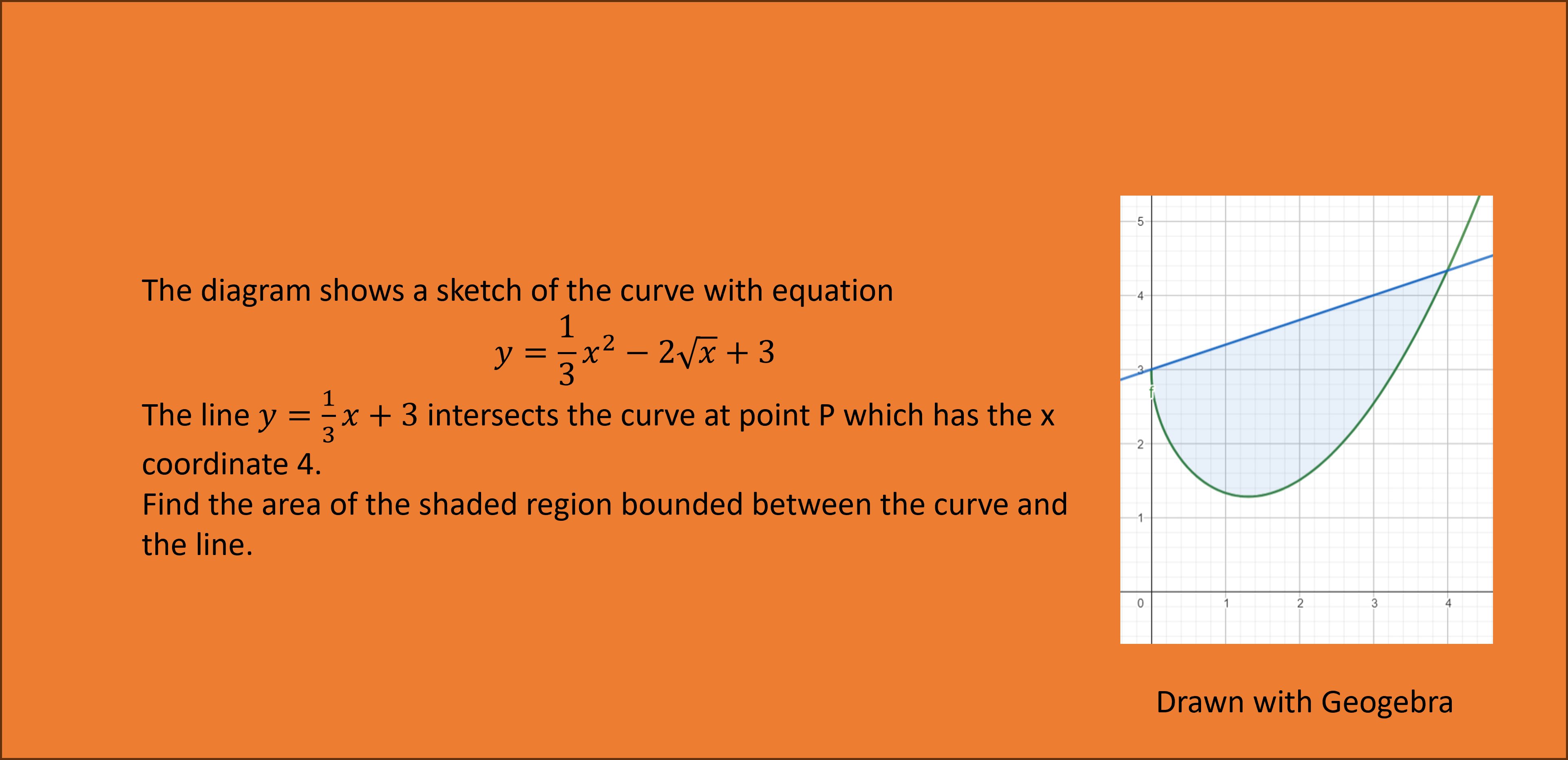
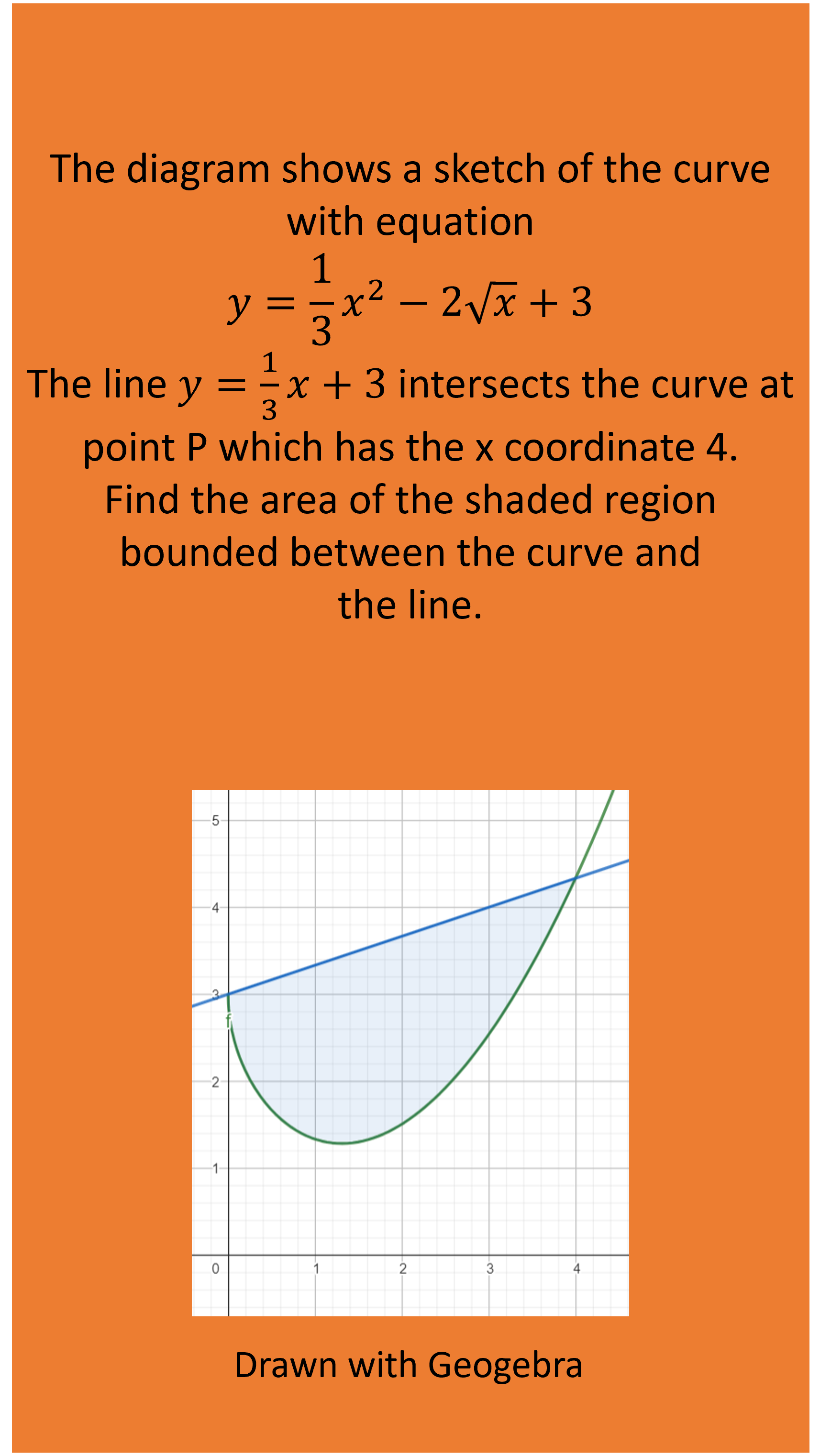
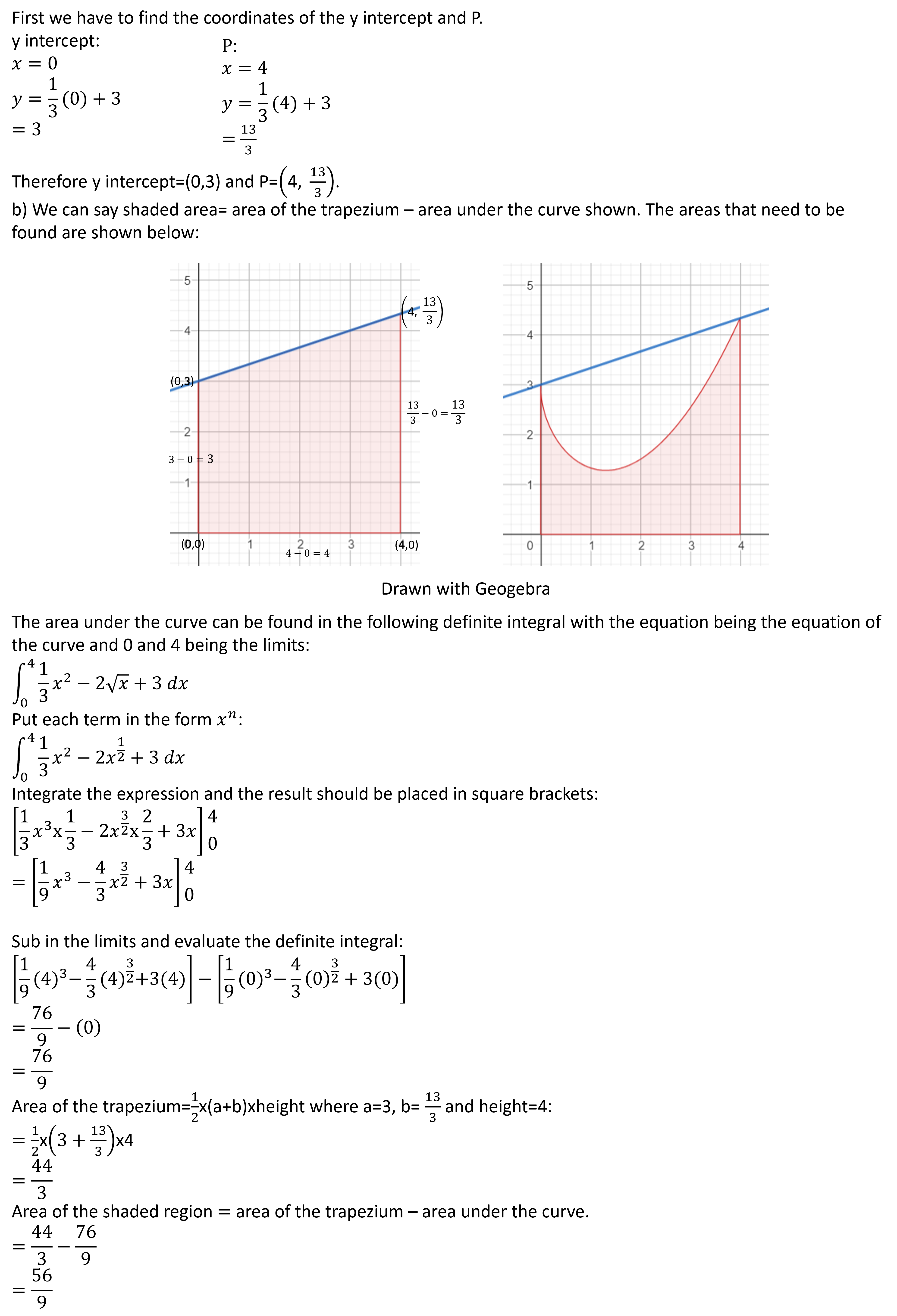
Image

Note: The diagrams shown in example 4 and the practice question with a red shaded region, are not necessary in terms of splitting them into seperate digrams. You can split the shaded region into different shapes in the diagram you will be given/you sketch.