Differential Equations

What are differential equations?

Differential equations are equations with derivative terms.

What are orders?

We can distinguish between different differential equations by focusing on the orders. For example, a first order differential equation has only first derivative terms and a second order differential equation has only second derivative terms.

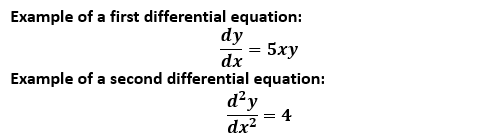
In the A Level syllabus, we only need to know how to find a solution to first order differential equations. To do this you have to seperate the variables in the following way:

The following solution is the general solution to the differential equation since a constant with no value is used. This means that it represents a family of solutions with different constants.

Example 1:

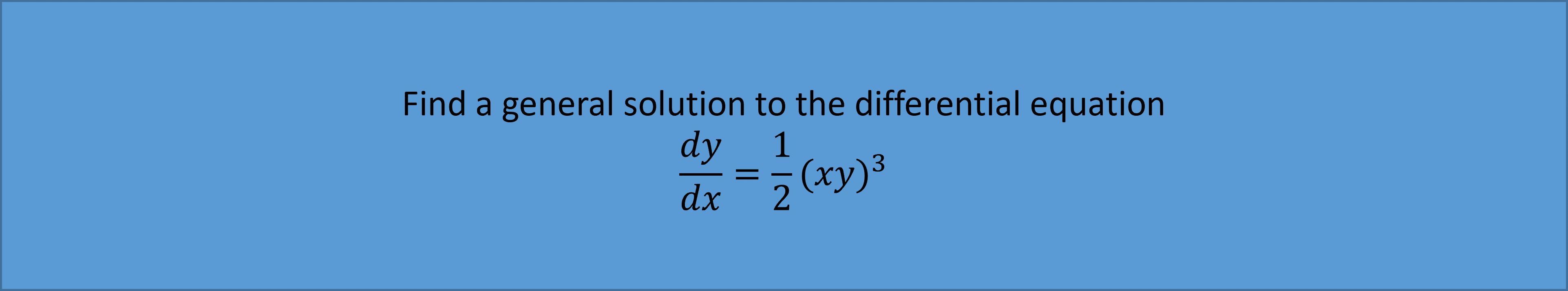
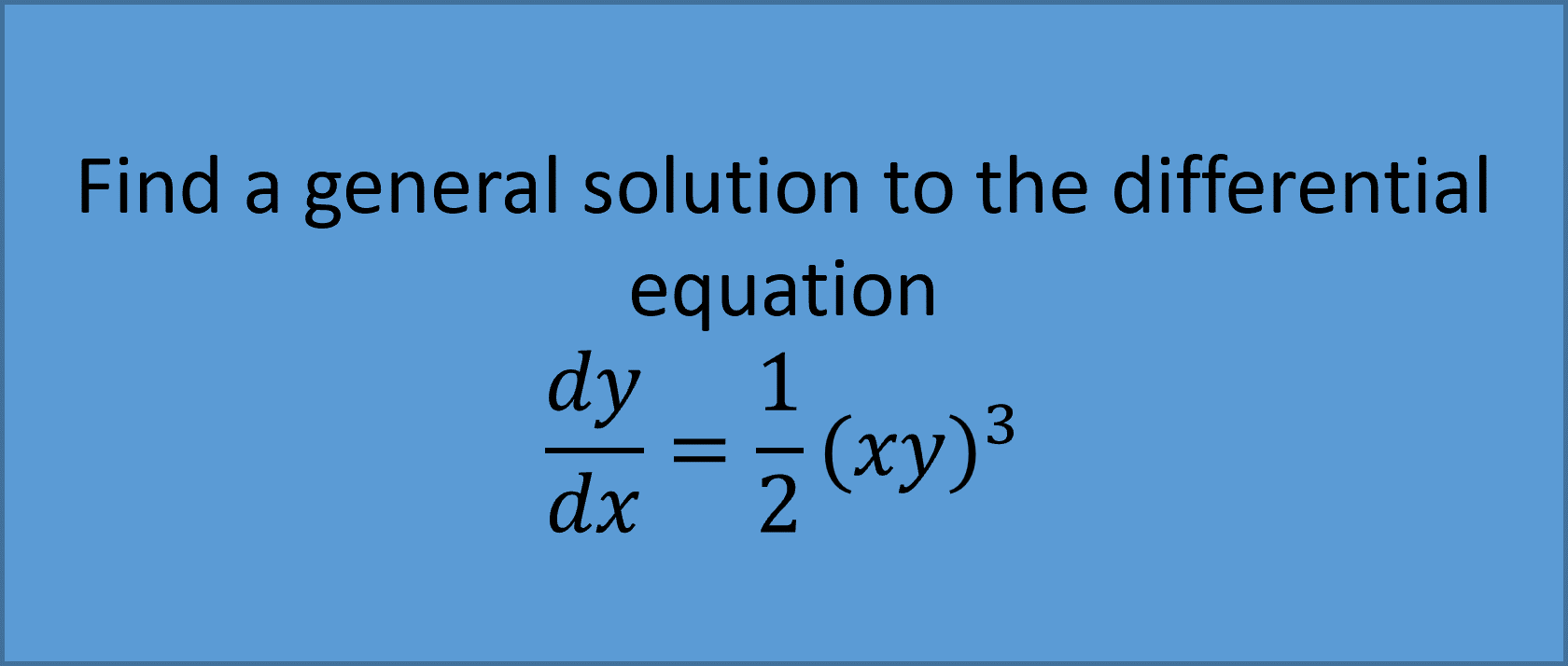
You can find specific solutions to differential equations if you have the coordinates of 1 point. This is sometimes called a boundary condition.

Example 2:

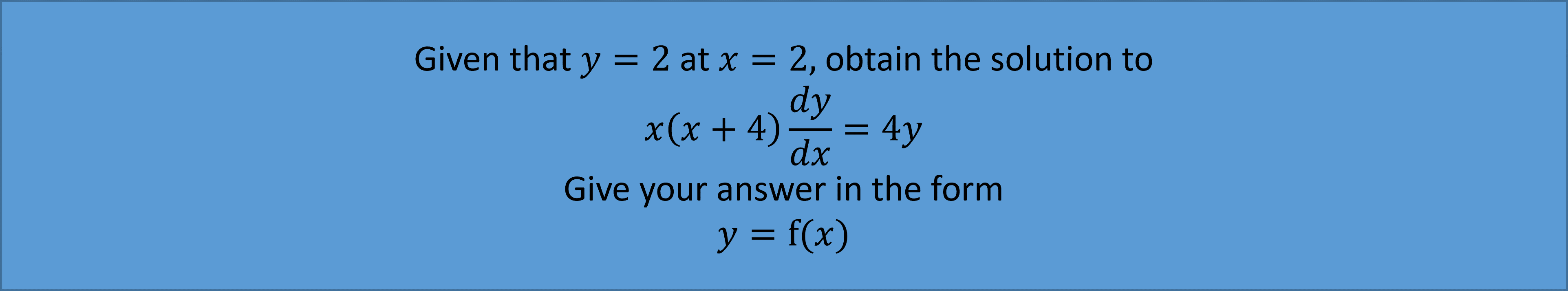
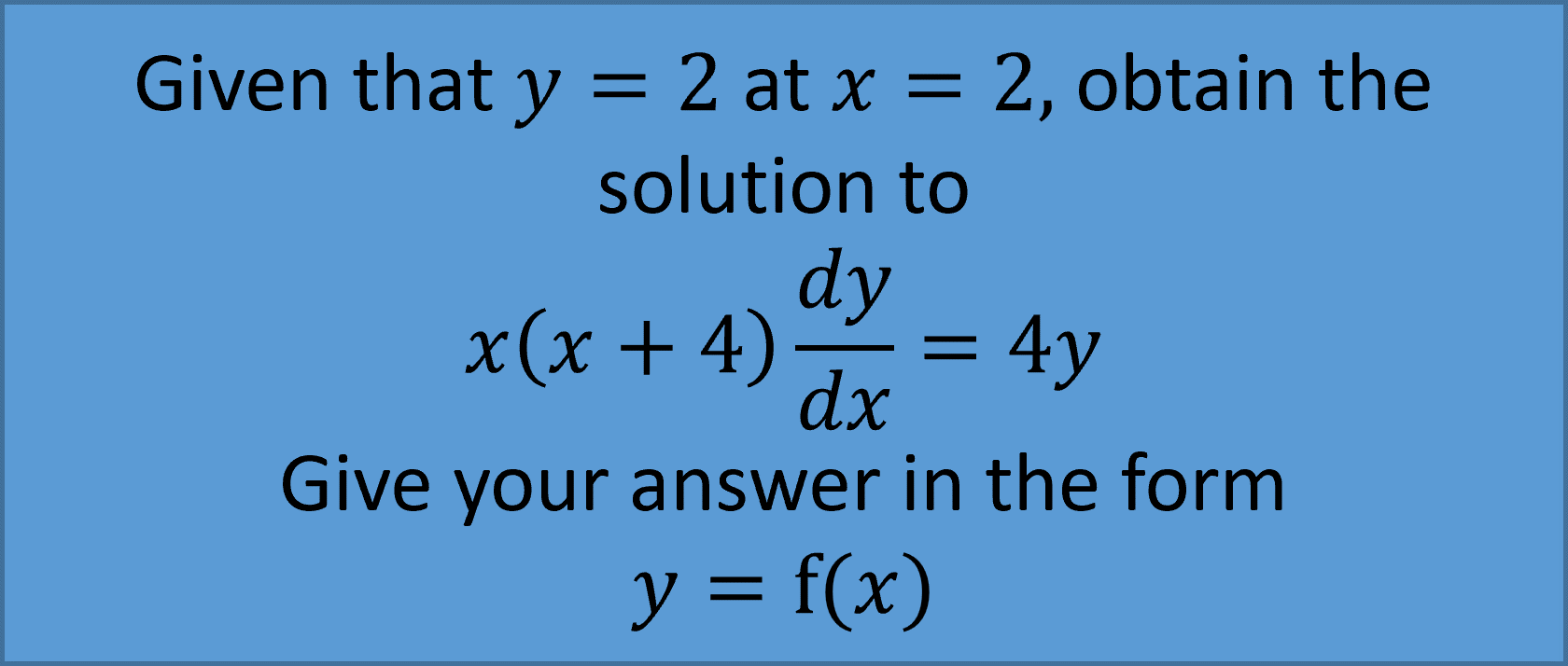
Modelling

In 9.10, you learnt how to form differential equations to model real life situations. Here you will learn how to find specific solutions and use the solutions in different ways based on the problem, whether it is to make predictions, find specific values and more.

Example 3:

It is important to understand the context of the model because you could be asked to comment on the model, mostly relating to limitations. Things that you can pick out based on the model include that a population has an limit, a container with water flowing out will be empty, shapes of objects in which a specific measurement is being monitored could change and you have to comment based on the question:

Let's look at the following question based on the previous example.

Example 3 continued:

You sometimes have to deal with multiple rates of change in a problem. Here you will most likely be asked/need to form a differential equation (which is a recap of 9.10) and then solve it. Thus for these problems, it is important to understand the context on how the different rates of change affect the overall rate of change, in order to form the differential equation as you will see in the next example.

Example 4:

Note: If you are given the differential equation but you are unable to prove it if asked, do not skip the solving part if you are able to solve the differential equation so that you don't miss all of the marks as usually this part of the paper will be worth a lot of marks.