Integration By Parts


Back to Integration Topics Page


For finding the integral of the product of two functions, you will need to use integration by parts.

The formula in function notation is:

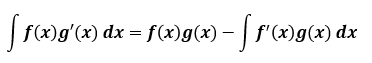
Note: This product as seen in the formula is the product of u and dv/dx.

How do you know which function is u and which function is dv/dx?

It will come with practice, but usually for expressions which contain xn, the u term should be the xn term. One case where it is different is an expression like x2lnx. Here the lnx term should be the u term, because it is difficult to integrate to find v if dv/dx is the lnx term. Likewise, if there is an ex term in the integral, it should be dv/dx, as it is easy to integrate that kind of term to find v.

Example 1:

Example 1
Answer 1
Example 2
Answer 2

Example 2:

Example 1
Answer 1
Example 2
Answer 2

Sometimes, you may need to use the formula twice in a question.

Example 3:

Example 1
Answer 1
Example 2
Answer 2

The following practice question is a difficult problem, with a trick at the very end.

Practice Question:





Image

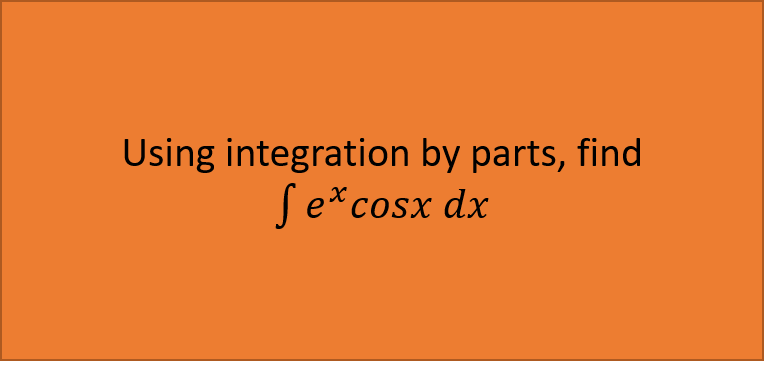
Note: Although the examples do not cover definite integrals, the process is the same to solve a normal definite integral. There is no need to convert limits, not like if you were integrating with substituition.