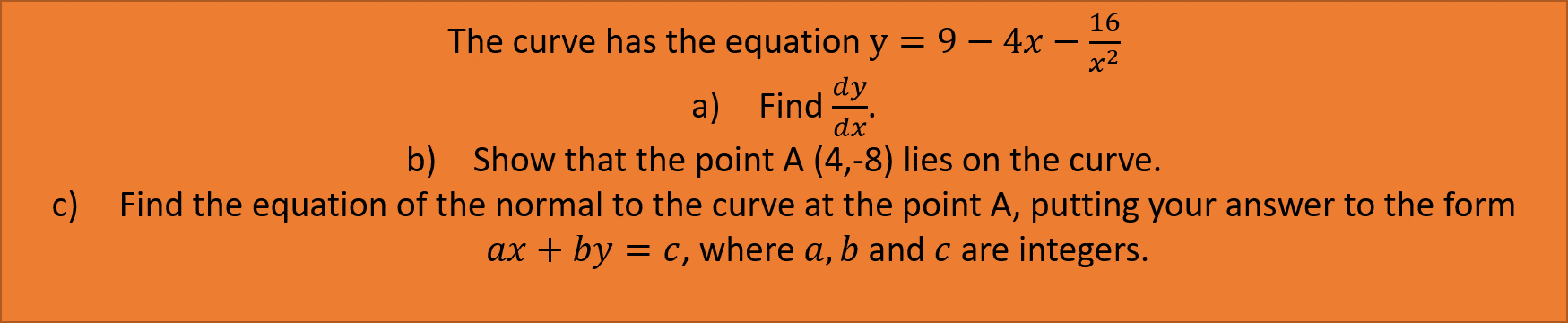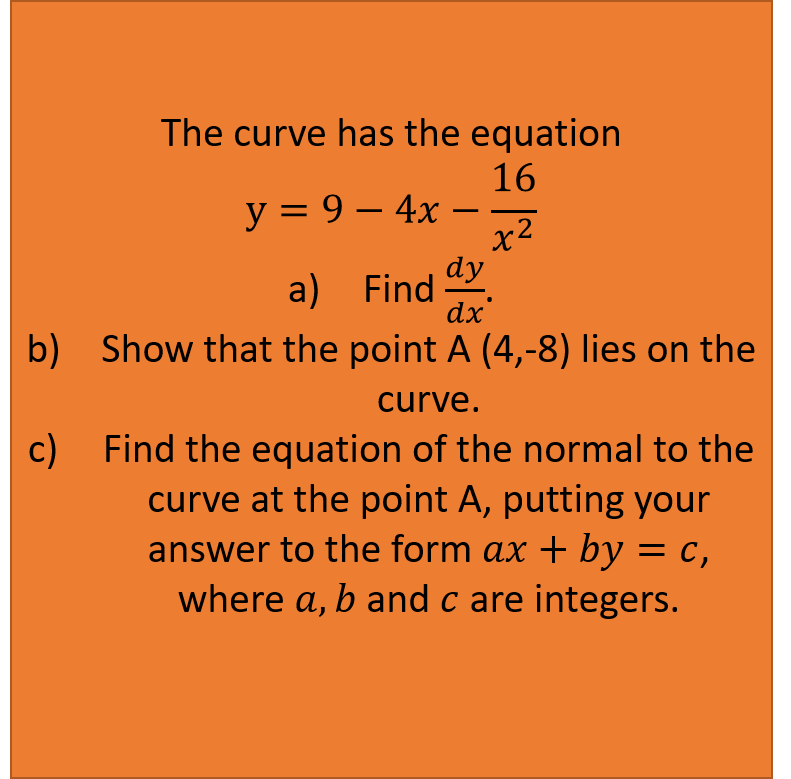Gradients, Tangents and Normals
Finding the differentiated expression and subbing in the x coordinate of the point into the expression will give the gradient of the curve at the point. Remember that the gradient of the curve is equal to the gradient of the tangent to the curve at that point. You can use this fact to find the equation of the tangent.
This means that for example for a curve with the equation y=f(x), the gradient of the tangent to this curve at the point with x coordinate a, the gradient of the tangent is f'(a). Therefore:

Note: This refers to the formula for finding the equation of a straight line y-y1=m(x-x1).
The normal to the curve at the point, is the straight line that is perpendicular to the tangent to that point. This means you can write the gradient of the normal as:
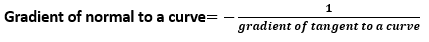
For the example of the curve with the equation y=f(x), the gradient of the normal to this curve at the point with x coordinate a, the gradient of the tangent is -1/f'(a). Therefore:
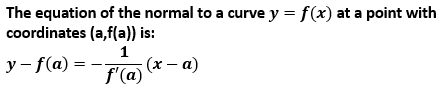
The difference between a normal and tangent can be seen in the graph below:
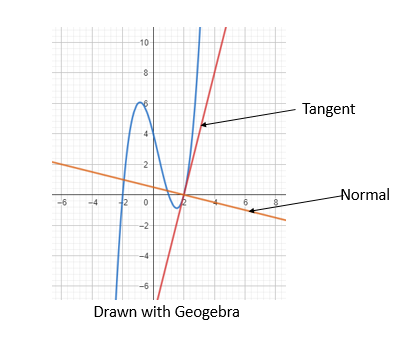
Example 1:
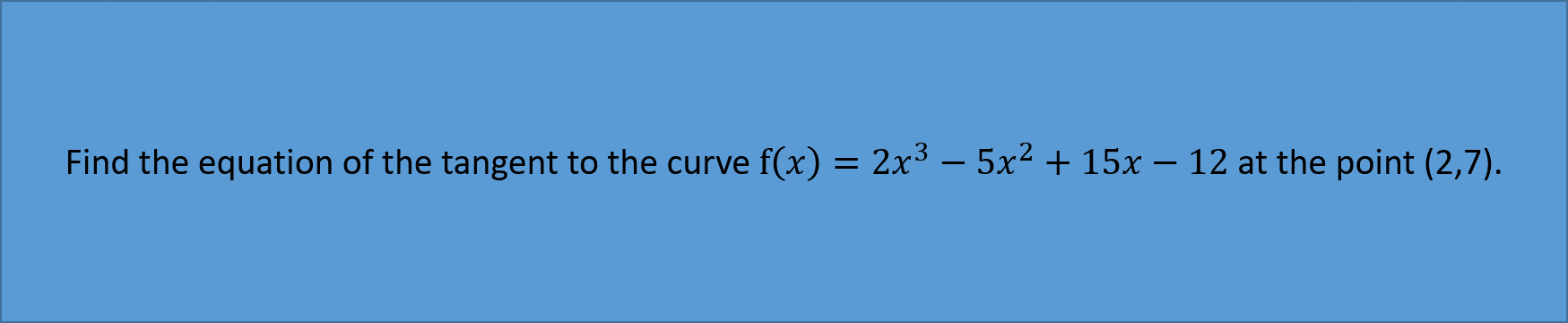
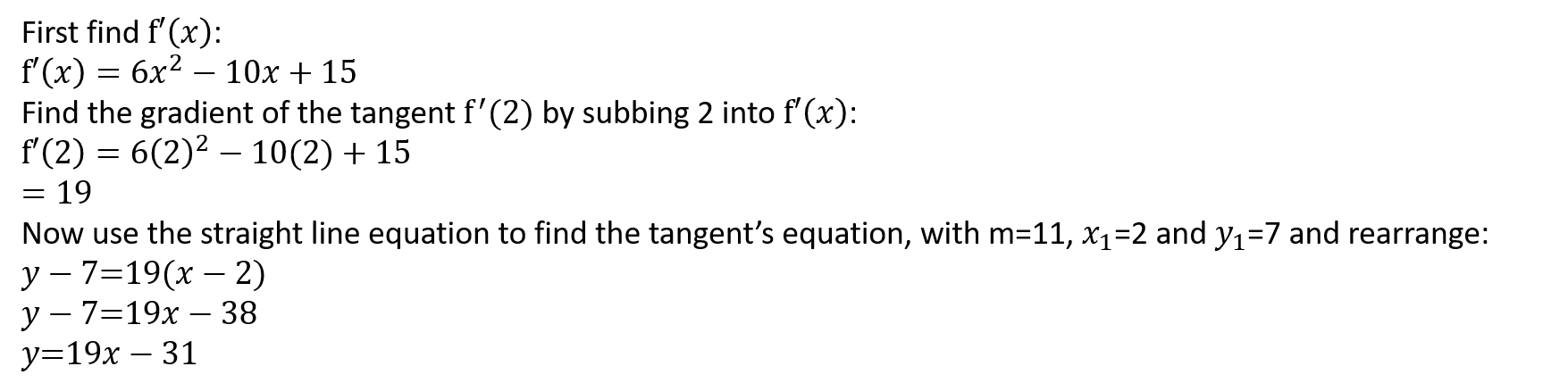
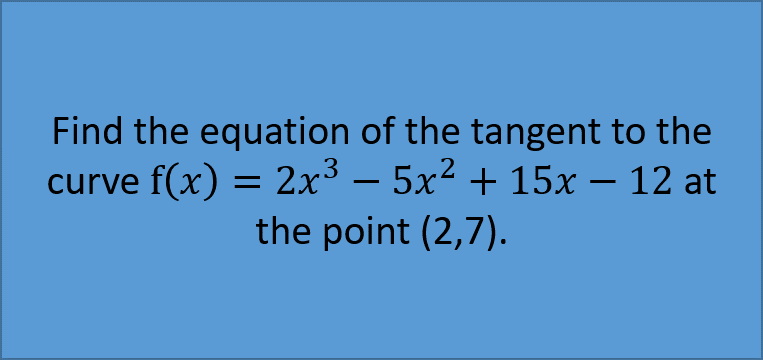

Example 2:
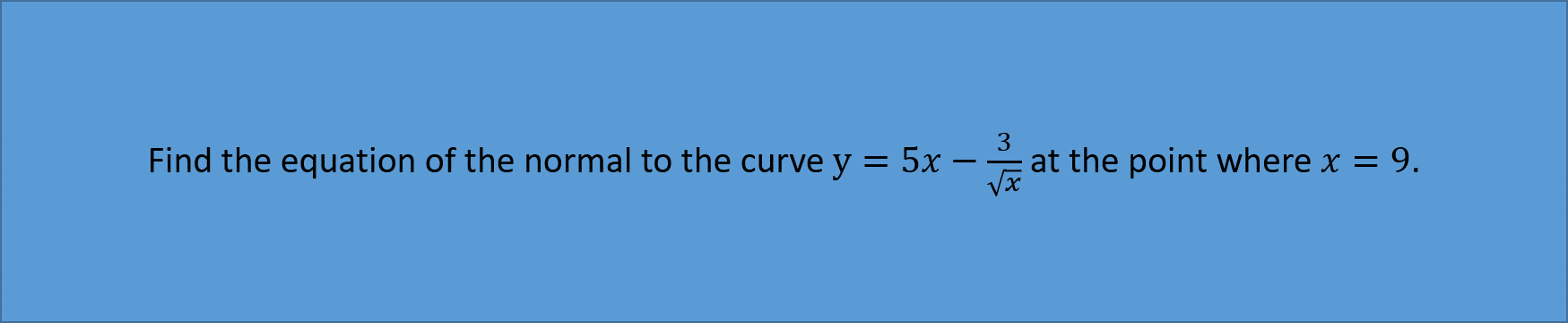

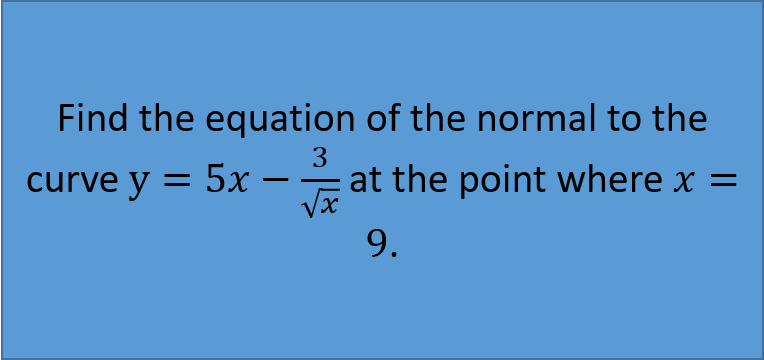

Practice Question: