Introduction to the derivative
How do we find the gradient of a curve?
The gradient of a curve is constantly changing. You can find the gradient of a point to the curve, by using the fact that it is equal to the gradient of the tangent to that curve.
What is a tangent in this context?
It is a line that just touches a point, without cutting or intersecting the curve. The tangent may intersect or cut the curve at other points of the curve. See the diagram below:
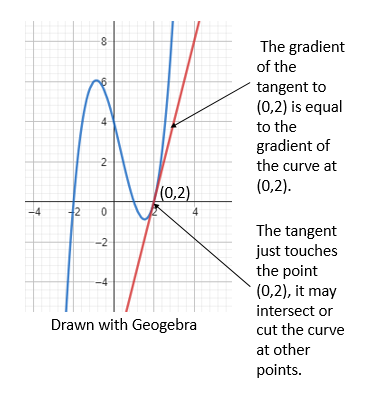
You can find the gradient of a curve at a particular point, by finding the gradient of the tangent to the curve at that point:
Example 1:


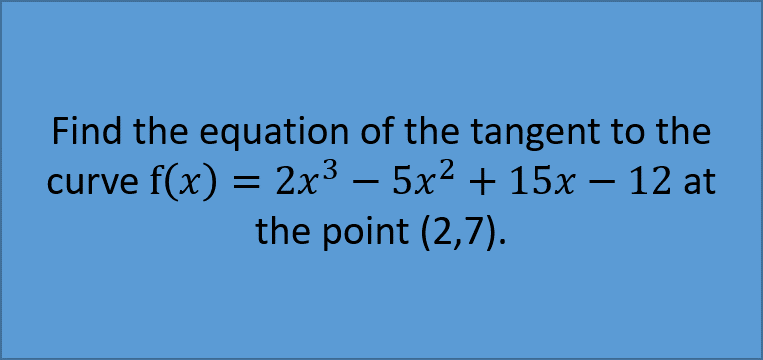
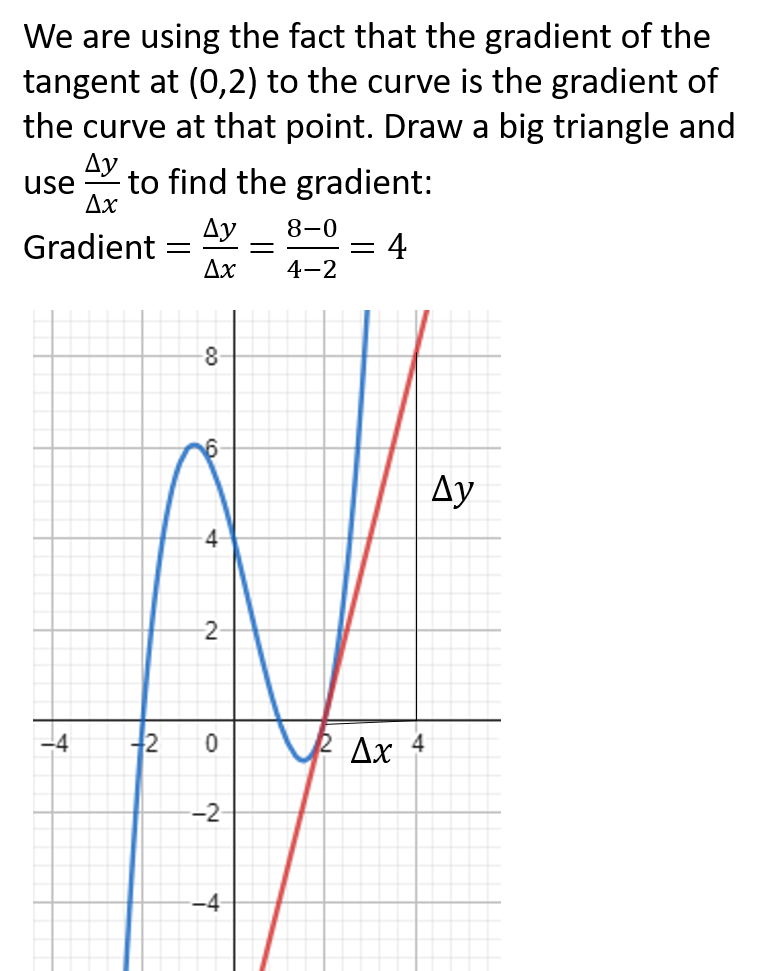
What is a derivative?
The tangent method above is one way of finding the gradient of a curve at a particular point. Another way is finding the derivative of a function.
The derivative of a function represented by dy/dx or f'(x) is associated function, that can be used to find the gradient of the function by subbing in the x coordinate of the point. This is why it is also known as the gradient function.
The process of finding the derivative of a function is called differentiation.
What is differentiation from first principles?
It is process of using a definition of the function f(x) to find the derivative:

The limh→0 refers to h tending to 0. This refers to the fact that, although h can't be 0 (as otherwise the expression will be undefined), as h becomes smaller, the expression will be more closer to the actual value.
Note: Don't worry if you don't fully understand the theory (from an A Level perspective). You need to ensure that you are solid with the proofs below as this definition is need to prove the derivative of an expression.
Example 2:




Note: Carefully understand each line of the proof, as for every question you will get, the concept is the same. Also to get full marks, you must add limh->0 for each line and finish off the proof like above to fully show the examiner how you get to the derivative from the definition.
Practice Question:

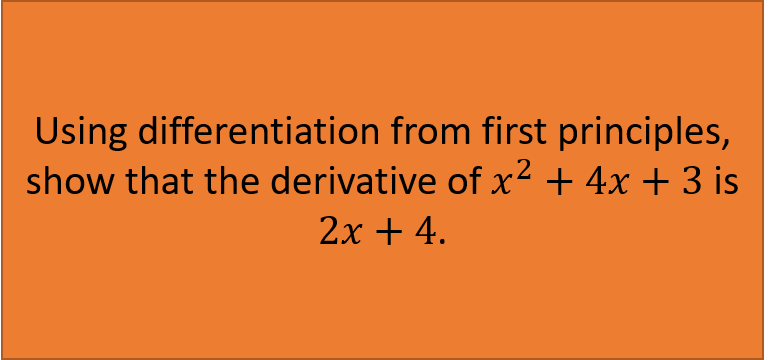


Note: This method of differentiating an expression is actually not the best way, but is usually the way examiners give questions on to prove a derivative, so you must fully grasp and understand it.