Implicit Differentiation

What are implicit equations?

Implicit equations are equations that contain both x and y terms. You will need to know how to differentiate these types of equations.

One case that you need to know to differentiate these types of equations is differentiating functions in terms of y with respect to x(derived from the chain rule):

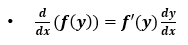
These following cases are more specific and useful to consider:

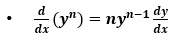
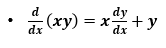
Note: This last case is just an example, but similarly you may get terms where it is an x function multiplied by an y function, so this is where you use the power rule.

Other things to remember include differentiating both sides of the equation as all terms must be differentiated and also you may have two or more dy/dx terms so you need to rearrange the equation to get the equation in terms of dy/dx.

Example 1:

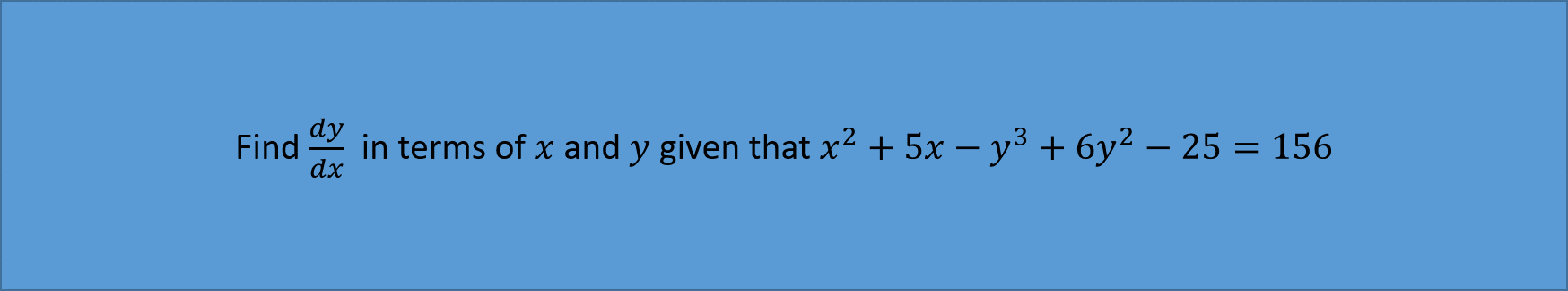
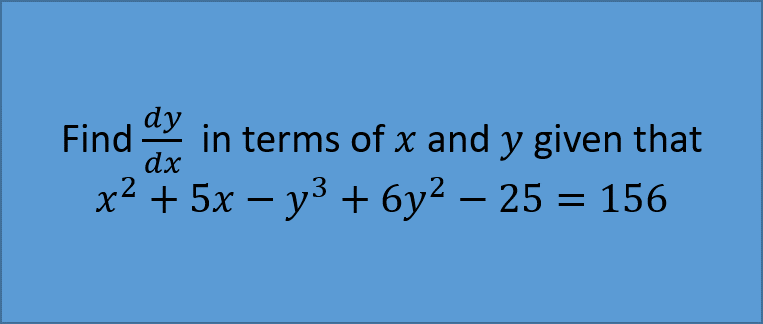
Example 2:

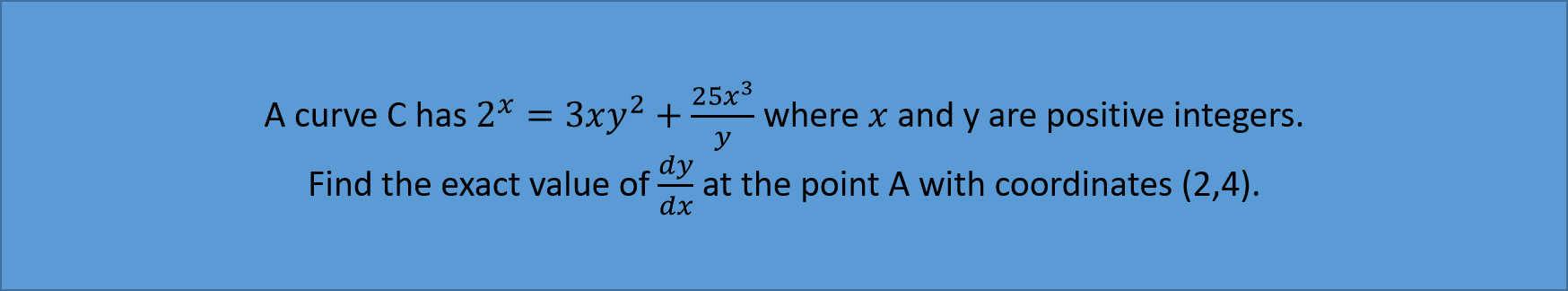
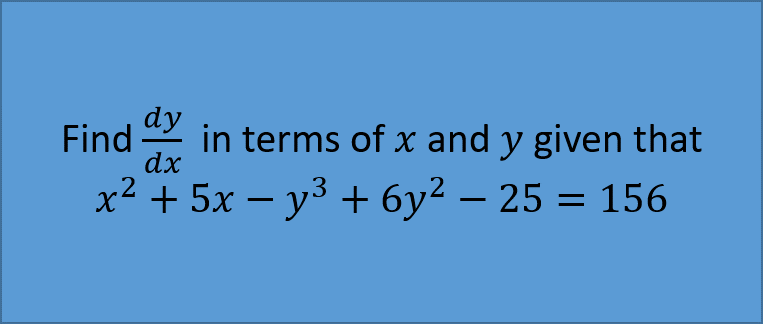
Note: Here you don't need to rearrange the algebra, as you are trying to find an value. However if you have to find values of stationary points, or leave your answer in algebraic form, the rearranging step is required.

Practice Question:

Show Answer

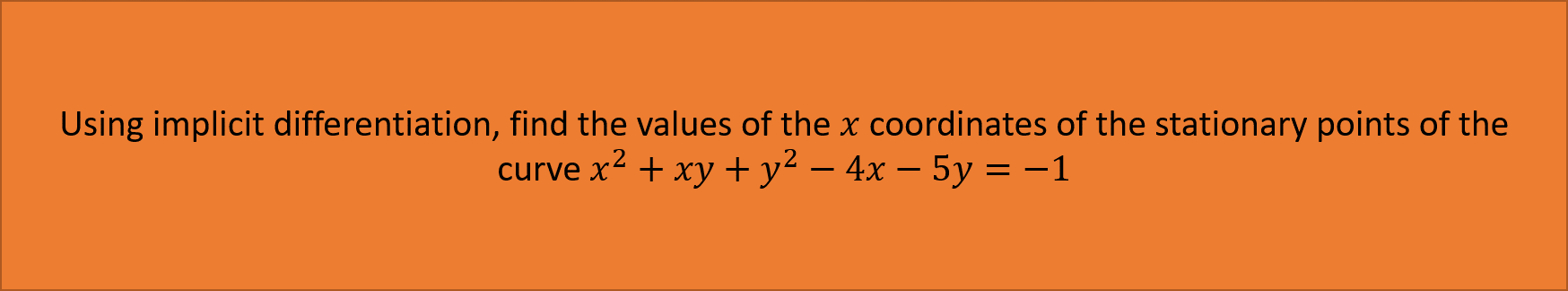
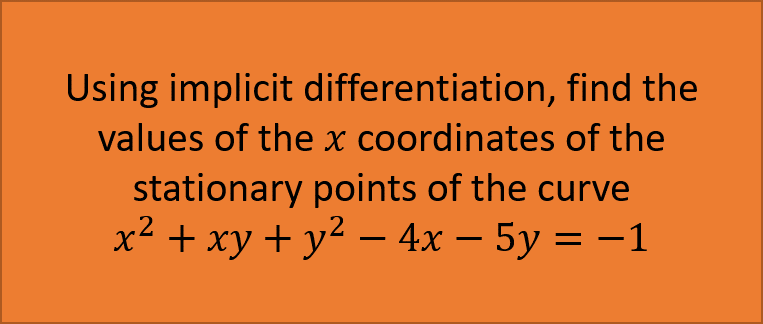
Note: Ideally you need to be aware of any rule or case that you have studied so far, for these types of questions as the examboard can use these types of questions to really test your understanding of differentiation.